
- TOP PAGE
- 攻略データ
- 基礎知識
- 関連情報
- OTHERS
ミニロトの当選となるケースは、1等から4等まで全3381パターンある
ミニロト抽選は、ロト用に開発された専用機「電動攪拌式遠心力型抽選機(愛称:夢ロトくん)」によって行われ、本数字5個とボーナス数字1個が抽出されます。その結果、例えば本数字が[07]→[23]→[04]→[30]→[14]、ボーナ ス数字が[19]といった順で数字が抽出されたとすると、ミニロトの抽選結果は右図のように決定(本数字の抽出順は関係ありません)し、以下のような当選パターンと確率、当選金額(各回の発売総額と当選口数によって変動)が確定します。
ス数字が[19]といった順で数字が抽出されたとすると、ミニロトの抽選結果は右図のように決定(本数字の抽出順は関係ありません)し、以下のような当選パターンと確率、当選金額(各回の発売総額と当選口数によって変動)が確定します。
 ス数字が[19]といった順で数字が抽出されたとすると、ミニロトの抽選結果は右図のように決定(本数字の抽出順は関係ありません)し、以下のような当選パターンと確率、当選金額(各回の発売総額と当選口数によって変動)が確定します。
ス数字が[19]といった順で数字が抽出されたとすると、ミニロトの抽選結果は右図のように決定(本数字の抽出順は関係ありません)し、以下のような当選パターンと確率、当選金額(各回の発売総額と当選口数によって変動)が確定します。  当選の条件は5個の申込数字が本数字5個とすべて一致
当選の条件は5個の申込数字が本数字5個とすべて一致 1等は、5個の申込数字が抽選結果の本数字5個とすべて一致した場合で、例えば上図のような抽選結果に対して、右図のような申込数字をいいます。1等にボーナス数字は関係なく当選のパターンは右図の一種類のみとなります。
1等は、5個の申込数字が抽選結果の本数字5個とすべて一致した場合で、例えば上図のような抽選結果に対して、右図のような申込数字をいいます。1等にボーナス数字は関係なく当選のパターンは右図の一種類のみとなります。◆ミニロトの数字5個による組合せは全169,911通り(後述)ですから、理論上1等の当選確率は1/169,911となり、理論値としての当選金額は約1,000万円(10,046,800円)です。
 当選の条件は申込数字が本数字4個と一致し、更にボーナス数字1個と一致
当選の条件は申込数字が本数字4個と一致し、更にボーナス数字1個と一致 2等は、申込数字5個のうち4個が抽選結果の本数字と一致し、更に残り1個の申込数字がボーナス数字と一致した場合で、例えば先の抽選結果に対して、右図のような5つの申込パターンになります。ボーナス数字は、この2等のためだけに抽出される数字のことで、他の等級には一切関係がありません。
2等は、申込数字5個のうち4個が抽選結果の本数字と一致し、更に残り1個の申込数字がボーナス数字と一致した場合で、例えば先の抽選結果に対して、右図のような5つの申込パターンになります。ボーナス数字は、この2等のためだけに抽出される数字のことで、他の等級には一切関係がありません。◆当選となるパターンは右図にある5つのパターンのみですから、理論上2等の当選確率は5/169,911から約1/33,982となり、理論値としての当選金額は約15万円(144,300円)です。
 当選の条件は5個の申込数字のうち4個が本数字に一致
当選の条件は5個の申込数字のうち4個が本数字に一致 3等は、申込数字5個のうち4個が抽選結果の本数字と一致した場合で、例えば右図のように、2等のボーナス数字がハズレたパターンをいいます。[else]ボールの部分には、本数字およびボーナス数字を除く25通りの数字がそれぞれ入ることになるので、25×5=125パターンの当選数字があることになります。
3等は、申込数字5個のうち4個が抽選結果の本数字と一致した場合で、例えば右図のように、2等のボーナス数字がハズレたパターンをいいます。[else]ボールの部分には、本数字およびボーナス数字を除く25通りの数字がそれぞれ入ることになるので、25×5=125パターンの当選数字があることになります。※[else]ボールは抽選結果(本数字5個とボーナス数字)以外の数字
◆理論上3等の当選確率は125/169,911から約1/1359となり、理論値としての当選金額は10,000円です。
 申込数字5個のうち3個が本数字に一致
申込数字5個のうち3個が本数字に一致4等は、申込数字5個のうち3個が抽選結果の本数字と一致した場合で、例えば下図のようなパターンをいいます。ここでは、抽選結果の本数字を外した[else]ボール2つのうちどちらかにボーナス数字が含まれていても関係ありません。下図の[else]ボールの部分には本数字を除く26個の数字の中から異なる2個の数字が入ることになるので、例えば最初の[else][else][14][23][30]で考えると26×25÷2=325通りあることがわかります。これが下図のように10個の組合せ全てに該当するので325×10=3250パターンの当選数字があることになります。

 ◆このことから4等の理論上の当選確率は169,911(全組合せ数)分の3250すなわち約1/52となることになります。
◆このことから4等の理論上の当選確率は169,911(全組合せ数)分の3250すなわち約1/52となることになります。
◆4等の当選金額は理論値としての目安になりますが1,000円となっています。

 ◆このことから4等の理論上の当選確率は169,911(全組合せ数)分の3250すなわち約1/52となることになります。
◆このことから4等の理論上の当選確率は169,911(全組合せ数)分の3250すなわち約1/52となることになります。◆4等の当選金額は理論値としての目安になりますが1,000円となっています。
MEMO
尚、以下の規定があります。
☆各等級間での重複当選は認めないこととし、上位等級を優先することとします。
☆すべての等級に当選者がいない場合は、再抽選となります。
☆当選金額は、発売額と当選口数により毎回変動します。
☆100円未満の端数は切り捨てられます。
☆各等級間での重複当選は認めないこととし、上位等級を優先することとします。
☆すべての等級に当選者がいない場合は、再抽選となります。
☆当選金額は、発売額と当選口数により毎回変動します。
☆100円未満の端数は切り捨てられます。
どんな夢(確率)に挑戦しているのか、ミニロト当選確率を検証しておこう
同じ数字選択式宝くじの「ナンバーズ4」なら、[0000]から[9999]までの数字の中から選択するので、その確率が10,000分の1であることはすぐに分かります。では数字選択式宝くじ・ミニロトのように[01]から[31]までの31個の数字の中から異なる5個の数字を選択するミニロトの場合はどうなのか。この計算はコンビネーションという式で計算することができます。例えば、8頭立ての競馬で連勝複式馬券(異なる2つの数字の組み合わせ)は28通りあることはよく知られています。これは、8個の数字の中から2個の数字を選ぶわけですから、
式は、8C2(コンビネーション8の2)となり、8P2(パーミュテーション8の2)÷2!(2の階乗)から
(8×7)÷(2×1)=28通り(的中確率は28分の1)となります。同じようにミニロト当選確率を計算すると、
31C5(コンビネーション31の5)=31P5(パーミュテーション31の5)÷5!(5の階乗)となり次のようになります。
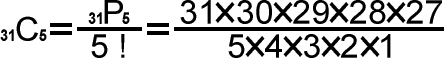
つまり、20389320÷120=169911通りの組み合わせがあり、内1等の当選パターンは1パターンのみですから当選の確率は169911分の1というわけです。さらに2等の場合は5つの当選パターンがあるわけですから169911分の5(1/33982.2)に、3等は169911分の125(1/1359.288)に、そして4等は169911分の3250(1/52.280・・・)ということになります。
式は、8C2(コンビネーション8の2)となり、8P2(パーミュテーション8の2)÷2!(2の階乗)から
(8×7)÷(2×1)=28通り(的中確率は28分の1)となります。同じようにミニロト当選確率を計算すると、
31C5(コンビネーション31の5)=31P5(パーミュテーション31の5)÷5!(5の階乗)となり次のようになります。
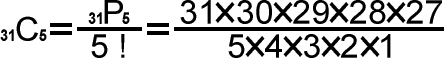
つまり、20389320÷120=169911通りの組み合わせがあり、内1等の当選パターンは1パターンのみですから当選の確率は169911分の1というわけです。さらに2等の場合は5つの当選パターンがあるわけですから169911分の5(1/33982.2)に、3等は169911分の125(1/1359.288)に、そして4等は169911分の3250(1/52.280・・・)ということになります。
| TopPageへ | ■■■ 攻略データ集 ■■■ | 本数字の合計値で9つのゾーンに分割 | ■■■ 関連情報 ■■■ |
| ■■■■■■■■ | 各数字の出現動向は出現分布図をみる | ■■■ 基礎知識 ■■■ | 数字にまつわるヒント・キーワード |
| 当サイトについて | 数字を追う所に出目データは存在する | 当選金決定の仕組みとプロセスを検証 | 時には色を見てミニロト予想 |
| データについて | 各数字の出現特性を立体グラフで解析 | ミニロトの購入方法を図解で紹介 | ここは一発!ミニロト大明神に神頼み |
| 紹介ソフトについて | 二つのグラフ比較で出現の予兆を探る | 当選パターンの種類と的中確率 | 過去の抽選結果や予想、一句鑑賞 |
| ■■■■■■■■ | 毎回ひと組の確率で出現する連続数字 | 1等賞金は最高4000万円まである | 1等賞金6億円を目指すならロト6 |